Move fast and break nothing

Translator’s Note: The organization responsible for tax collection and calculation is the Direction Générale des Finances Publiques or the DGFiP. In what follows, I have decided to continue using DGFiP.

Editor’s Note: Many thanks to Dhruv Sharma for his invaluable translation help.

In my last blog post, I had mentioned my attempts at using the source code for the income tax, published by the tax authorities in France. At the time, I stated the following:

At this moment, however, the code generated by Mlang is still incorrect. Indeed, a side effect of this formalization and validation work was to discover that the M code published by the DGFiP does not contain all the information needed to reproduce the tax calculation. Technically, M code is called several times with particular values for certain variables. This technical subtlety had not been detected during the hackathon and the first publication of the code. I was able to inform the DGFiP, who are currently implementing changes to allow me to recover information about these multiple M-code calls with different parameters. Once I have this information, I will be able to complete the work of formalizing and validatig Mlang on the official test data of the DGFiP.

One year later, and I have kept my promise! Mlang, the new compiler for the DGFiP’s in-house programming language “M”, is operational, and allows you to reproduce the tax calculation at home just as it is done at the Bercy taxation office. This allows you to check your last tax returns and how your income tax is calculated! For example, this line applies the progressive scale of tax after applying the family quotient. Of course, not everything is smooth sailing and it would be necessary to rewrite everything for it to understandable; but that’s for another time…

Even better, the DGFiP itself is taking a step towards greater transparency and embracing modern coding standards : Mlang will eventually become the official compiler used in production for calculating income tax! Move fast and break things is the credo of “disruptive” computer scientists in the fast-paced world of startups; here, it’s more about doing the opposite , Move slow and fix things, because we can’t afford to break the calculation of the income tax. Getting there however means that the traditional methods of project management must be broken.

In this post, I propose a deep dive into the heart of the tax calculation computation, and thereby understand how our field of research of formal methods allowed Raphaël Monat and me to create a modern and operational alternative to a critical component of the DGFiP’s computer systems. My objective for this article to provide enough details for you to then be able to read and understand our research article (co-written with my thesis supervisor Jonathan Protzenko). Hopefully, this post will also make clear the advantages and disadvantages of the programming languages used.

Finally, I will also stick my neck out and say the following: while the current industrial vision of management information technology is based on mass employment of low-skilled programmers, I advocate for employing qualified software craftsmen for critical projects. Tl;dr: don’t hesitate to hire more programming language specialists to maintain your critical software!

An unusual architecture

The Legacy of 30 years of use

The DGFiP has, among its many missions, the right to levy income tax . The amount of tax depends on income of the household and follows a progressive scale. Every year, French households send their returns to the DGFiP, the vast majority of which are filed using a form available on impots.gouv.fr. This form, which French readers have probably seen before, has multiple boxes allowing you to to differentiate the sources of income: several hundred boxes in fact. Moreover, tax law has a lot of exceptions that must be taken into account when calculating income tax. One could debate the relevance of an simplifying these exceptions, but that doesn’t concern us here.

Once the tax declaration has been received, the DGFiP has everything it requires to calculate your income tax. What happens then? All the values filled in the boxes of the declaration are transformed into input for a very special computer program, which calculates the tax according to the legislative rules of the General Tax Code. Note that this process is different from the US, where people have to manually compute the amount of tax they owe or use the services of a private company to do so.

If we talk of programs, can programming languages be far behind. And this is where the DGFiP does something unusual: since instead of coding the program in C, Java, Python or another established language, they have chosen the M language. What is the M language? It is a “dedicated” language (domain-specific language or DSL) created by the DGFiP, for the DGFiP in 1990.

Indeed, here is an excerpt from the published source code:

rule 521010:
application : bareme , iliad ;

for x=0,5;y=1,2;z=1,2:
DSxyz = somme(i=1..9: max(QFxyz - LIMINFBARi, 0) * (TAUXi / 100)) ;

Even without knowing the M language, we can observe that there are loops, an addition operator (somme is addition in French) applied to the maximum operation multiplied by a rate (TAUX). Indeed, this piece of code calculates the amount of tax to be paid (“droits simples”, DS) based on the family quotient (“quotients familiales” or QF) and the rates of the different brackets of income tax.

Even though it might appear somewhat spartan at first glance, the M language was designed for specialists in tax laws: it allows rules for calculating taxes to be expressed in a concise manner. When it was redesigned in 1990, the aim was to enable tax law specialists at Bercy to read and write the M code directly, without having to go ask computer scientists or programmers for help.

Code written in M has thus existed for 30 years, and is updated every year after the vote of the Finance Bill that modifies the scale and terms of the income tax in France. However, the laudable objective of dispensing with programmers had to be abandoned along the way, since it is a team of computer programmers and other experts from the DGFiP’s SI-1E office that is currently responsible for the maintenance and evolution of the code.

Let’s go back to how the tax is calculated. Among the variables in M, some of them are values that are found on the tax return, others are intermediate variables, and finally a handful correspond to the amount of tax to be paid, such as IRNET (Impot sur le revenu Net or Net Income Tax). It then suffices to calculate the values of the variables one after the other to arrive at the final result. Simple isn’t it?

Not so fast! To execute a program written in M, we first need to translate it another language that the machine understands. In 1990, when M was created, the DGFiP chose C as the target language. Therefore code written in M is translated into C code thanks to a compiler that we will call compIRateur before executing it. At the time, C was a “high-level” language with a mature ecosystem, so this choice is quite reasonable.

To complete the picture, we need to supplement the published M code-base with a set of unpublished files with a mysterious name “INTER”. These INTER files were not readily available and hence I was unable to reproduce the calculation in my previous post.

These INTER files are written in C and interact directly with the C translation of the M files. They contain the logic of a tax law mechanism called “multiple liquidations”. This involves recalculating the tax several times in a row with different entries to, for example, cap the amount of tax benefits, or the benefits related to the family quotient.

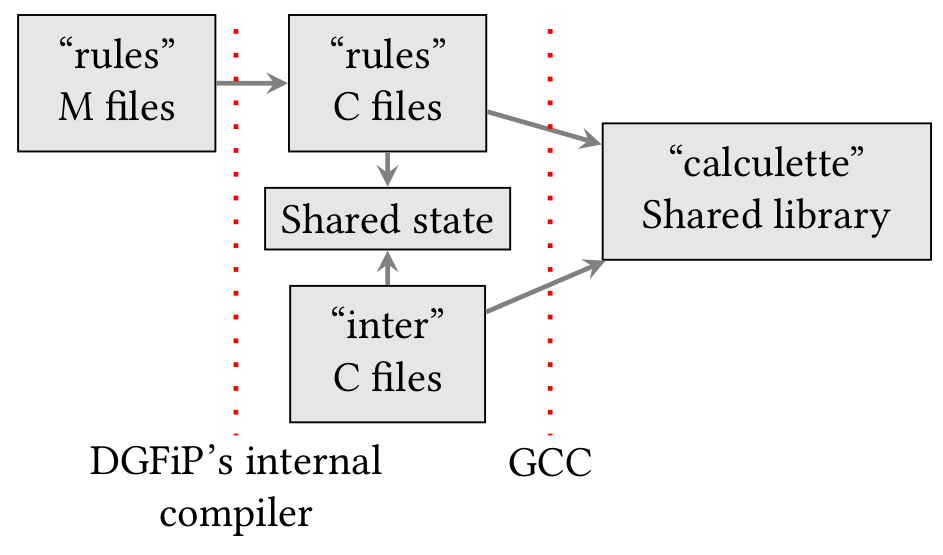
M language, M files, INTER files written in C; all this seems very complicated. Wouldn’t it have been easier to write everything in C from the get-go?

Why use a dedicated language?

This question is quite pertinent; let us stop for a moment to examine the case for choosing the M language in 1990, and understand its pros and cons. A crucial driving the choice of the language is the nature of the problem to be solved: the calculation of taxes. A program that calculates tax is not just any computer program, and one can make indeed strong hypotheses about what is needed in a language to write such a program.

First hypothesis: the tax calculation always terminates. Therefore, there is a priori no need for general recursion or infinite loops to write the program. Second hypothesis: the tax calculation rules are simple enough to be expressible using basic arithmetic. The second hypothesis is more debatable than the first, because the imagination of the tax legislator is boundless. Let us suppose it to be true, as the DGFiP surely did in 1990.

Under these hypotheses, a dedicated language or a domain specific language (DSL) seems like an attractive solution since it places constraints on how the developer writes code. In this case only basic arithmetic rules on variables: no pointers, no functions, no data structures. And this limitation is crucial for respecting a major constraint of the DGFiP: performance. Indeed, we must calculate a household’s tax contributions in a few milliseconds. This constraint is necessary because, with 37 million households, each calculation has to be done very quickly so that the total time doesn’t explode.

By using only arithmetic expressions, without conditionals, the code used by the DGFiP is exceptionally fast: the 600,000 lines of C code generated by the compIRateur run in just one millisecond. This remarkable performance is due to the generated C code, which uses several ingenious tricks; for instance grouping the M variables into a large array that fits into the processor cache to optimize memory accesses.

Another advantage of using a DSL is that the M developer does not need to specify the order in which the variables are calculated. The compIRateur reorders automatically the variables following the order induced by the dependency graph of the code. And with more than 27,000 variables, this functionality is extremely practical since the legislation that the code is supposed to follow does not define the variables in the order in which they are calculated. Concretely, imagine that you have X = 0, Y = X + Z and Z = 2 * X. By analyzing the dependencies between the variables, we deduce that we have to calculate X first, then Z and finally Y.

This last point on dependency computation also explains why the DGFiP chose an external dedicated language, with its own syntax and compiler, rather than a dedicated language embedded inside C, based on pre-processor macros that emulate the M syntax. As powerful as the C pre-processor macros are, we can’t use them to compute the topological order of a dependency graph. For doing this, a real compiler is required.

However, the choice of DSL also comes with its share of drawbacks. Firstly, a dedicated language necessarily starts in a niche market, is not taught at university and it is therefore necessary to train developers internally. Fortunately, the M language itself is not very complicated, so training developers in it is not a major obstacle. Second, there is a lack of tooling. A programming language comes with a tool to help with essential aspects of programming: syntax highlighting, static analysis connected to integrated development environments (IDE), etc. The M language does not have such tools, because of the small number of people using it. But in 1990, the very notion of tooling for programming languages beyond the compiler was in its infancy; this disadvantage must have seemed minor at the time.

Third and most importantly, the strength of a DSL is also its weakness: by restricting the language to assignments of variables by arithmetic expressions, the M language deprives the programmer of any tool that might help in creating abstractions. In particular, the absence of user-defined functions leads to the need to duplicate the code. Duplication of code is the deadly enemy of the programmer, because it makes it difficult to maintain a code base where any modification must be replicated in multiple places, combined with all the risks of forgetting and error that this entails.

It is this reason — the lack of functions in the M language — which led to the creation of the C INTER files that serve various functions: the fiscal logic of multiple liquidations leads us to formalize the liquidation of the tax as a function to be called with different parameters, which is impossible to express in M without duplicating code.

Modernizing without breaking things

So it was this legacy architecture that Raphaël and I discovered when we were able to access the DGFiP’s complete unpublished source code. From then on, Mlang’s initial objective, which was to render the M code published by the DGFiP usable, became much more complex. Indeed, in order for this published M code to be usable, Mlang also had to integrate the work of the INTER files which in turn will never be published for security reasons.

At this stage, we had extensive discussions with the programmers at the DGFiP. It was from these discussions that we were able to understand the history of the situation, as well as the various constraints on the project. It quickly became apparent that the initial objective of Mlang overlapped with an internal goal of the DGFiP: to maintain control over the compilation of the M language. Indeed, after 30 years of operation, the original developers of the DGFiP’s compIRateur are retiring, which would be an enormous loss. Furthermore, the source code of the compIRateur we were able to access, written in C and in 1990 for the most part, is somewhat obsolete compared to good compiler writing practices of today. The creation of Mlang was therefore a very good opportunity for the DGFiP to modernize an essential piece of software within the income tax computation architecture.

An incremental approach

One of the imperatives of any attempt to modernize the income tax calculator is incrementality. The income tax calculator is at the heart of the DGFiP’s IT system, and myriad applications are embedded in the tax calculation module: online simulator, business software for advisors at local public finance centers, etc. It is therefore necessary for the modernized solution to keep the same interface for its applications, concretely a C interface.

Equally important, any modernization must take into account the management of the IT and tax skills needed to transform the legislative texts governing the calculation of the income tax into computer code. Currently, the DGFiP has the ability and a proven code base with the M language. Switching from M to another traditional programming language would mean rewriting the tax rules in a language not necessarily adapted to the form of the tax rules. In another similar context this time concerning the payroll rules for army soldiers, a modernization initiative called Louvois has shown the dangers of minimizing the complexity of these rules by considering such a rewrite as an IT project like any other.

Despite these constraints, incremental modernization can bring new functionalities to the IR calculation system, for example:

• a precise measurement of the coverage of the tests, especially at the level of the individual values of the M variables;
• newer targets for compiling the M language, to facilitate interoperability with other government computer applications;
• an analysis of the accuracy of calculations using floats.

A new architecture centered around the compiler

The path to modernization we propose with Raphaël and Jonathan is based on Mlang and more generally on the compilation between different languages, as a sequence of connecting links between the different components of this complex architecture.

First, Mlang is a complete compiler for the M language, based on formal semantics obtained by reverse engineering. This semantics is presented in our research paper and provides the implementation details for Mlang. For example, unlike the original compIRateur of the DGFiP, Mlang has an M interpreter that serves as a reference to the language: debugging is first done using the interpreter which has adapted functionalities (displaying variable values, etc.). Once the bug is fixed using the interpreter, then the behavior should be correct in each of Mlang’s target languages (C, Python, etc.). This separates the problems, allowing the user to know if their bug comes from M code or from the compiler.

Second, we have improved Mlang to manage and replicate the functionalities implemented in INTER files not published by the DGFiP. For this, we have studied the code of the INTER files at length in order to determine exactly what these files were doing. In the INTER files, an essential data structure is updated throughout the code performing multiple liquidations: the general table of values, or TGV (French for Tableau Général des Valeurs). The TGV is an array in C which contains the values of all the variables declared in M code. As the M-translated C is executed, the TGV is updated. When the INTER code calls the M code, it passes as input the “empty” TGV which contains only the input variables of M (corresponding to the details entered on the tax return), and receives in return the TGV “filled” with the calculated values.

When we examine the code of these INTER files, we observe that their role is to call the M code several times, while managing the status of the TGV between the calls by saving the value of certain variables or by modifying the value of special M variables that look like flags activating or disabling parts of the M code. But, because the C language is very low level, we realized that the pure logic contained in the INTER files was relatively simple, but hidden within the large mass of standard C code to manage pointers and mutable state.

So we decided with Raphael and created a second dedicated external companion language to express the logic contained in the INTER files. This language, which we named M++, looks like this:

compute_benefits():
 if exists_deposit_defined_variables() or exists_taxbenefit_ceiled_variables():
    partition with var_is_taxbenefit:
      V_INDTEO = 1
      V_CALCUL_NAPS = 1
      NAPSANSPENA, IAD11, INE, IRE, PREM8_11 <- call_m()
      V_CALCUL_NAPS = 0
      iad11 = cast(IAD11)
      ire = cast(IRE)
      ine = cast(INE)
      prem = cast(PREM8_11)
      PREM8_11 = prem
    V_IAD11TEO = iad11
    V_IRETEO = ire
    V_INETEO = ine

The syntax looks a lot like Python because M++ resembles a scripting language. M++ has functions, conditionals, variable assignments and a special function: call_m. Variables in capital letters are TGV variables in M code while others are local M++ variables.

Using a dedicated high-level language such as M++, Raphaël and I are able to express more than 5,500 lines of INTER C code (including comments) in a hundred lines of M++. We therefore believe that the maintenance of M++ code will be considerably easier than M code. Moreover, M++ is intimately linked to M through Mlang. Indeed, inside Mlang, calls to call_m are simply inlined in the same intermediate representation. Here is the architecture of Mlang, structured by numerous intermediate representations:

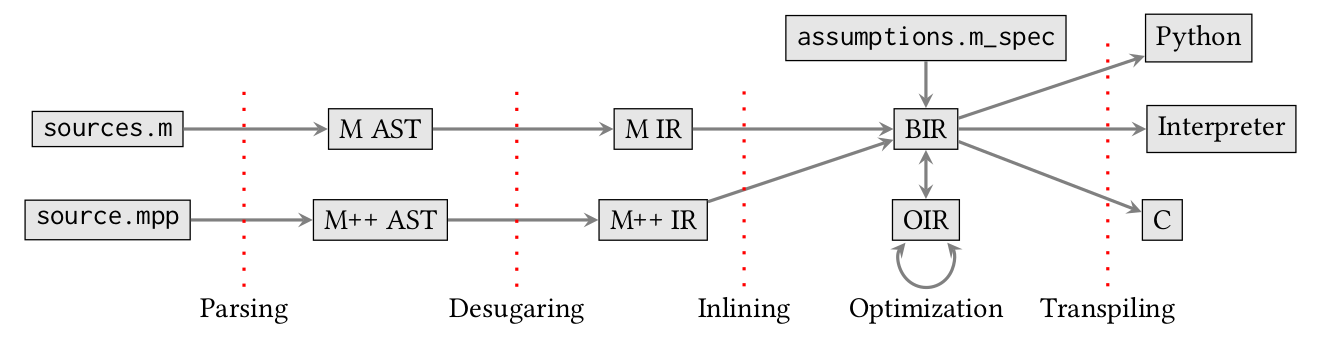
M and M++ are merged in the BIR representation, which makes it possible to consider in a single program all the source files containing the tax calculation logic, irrespective of whether they are written in M or M++.

The M++ language does not seek to be elegant in its design, and doesn’t follow a traditional programming paradigm in particular. On the contrary, it is a completely ad-hoc tool that adapts to the particular situation expressed within INTER files. By creating a dedicated language from an existing codebase, the approach is to extract the essentials, the logical meat if you will, from the codebase and leave out everything inessential. The passage from the C of the INTER files to M++ limits de facto what can be expressed, which is always the case when you switch from a generalist language to a dedicated language. But the analysis of the history of the INTER files, which reflects the evolution of French tax law, suggests that there will be no need for a new functionality of the language as long as we continue to function within the existing paradigm of tax calculation.

However, it is quite possible that the tax legislation evolves which introduces a complexity within the tax calculation such that M and M++ will in turn be insufficient to express the calculation numerically. In this case, and thanks to the formal mastery of both languages, it will nonetheless be possible to add a functionality adapted to the language and thus ensures maintainable, durable code.

Without breaking anything?

Throughout the process of developing our solution around Mlang, we were treaded meticulously and took pains to ensure that we were not breaking the income tax calculation.

For this purpose, the DGFiP provided us with all of its private test datasets. The DGFiP’s test sets consist of a large number of (fictitious) tax households (between 500 and 1000), normally written by tax lawyers who calculate by hand the amount of tax due. Mlang is thus validated on these test sets, for the calculation of the 2018 and 2019 income tax. During the next stages when Mlang will be considered to be put in production, the results from Mlang can be compared with those of the old system on the data from all French tax centers, thus providing a maximal guarantee for the transition to the modern system.

However, this only concerns the internal validation of Mlang. Raphaël and I wanted to make sure that Mlang’s evaluation could be replicated independently from the DGFiP’s datasets. However, the DGFiP did not want its test sets to be made public. So we had to find a solution to create new test sets, distinct from those of the DGFiP.

It would have been rather difficult for us to write test cases by hand, since we know nothing about tax law. We therefore decided to use another classical software engineering technique: fuzzing or random data testing. The principle is as follows: we randomly generate tax returns from tax households until one of the tests corresponds to a realistic tax household, which becomes a test set in its own right. These test sets are then validated by observing the results calculated with the older DGFiP system. Several questions arise immediately: What is a “realistic” tax household? How many test sets need to be generated to “cover the code completely”?

We considered a tax household to be “realistic” as soon as it raises none of the error conditions that are checked in M code. These conditions,of which there are 500, are used to validate the consistency of the tax return. For example, when box A states “share of income from box B dedicated to …”, then the amount in box A must be less than the amount in box B. The purpose of fuzzing is to find test data that satisfy these 500 conditions involving hundreds of input variables, which is far from being a straightforward exercise!

To obtain quick results, we use a rather clever fuzzing technique based on the AFL tool. In this fuzzing guided by the coverage of new execution paths in the tested binary file, the random generation is biased towards test cases that lead to results that are different from all previous attempts. This simple idea refined by numerous heuristics allows for random exploration to quickly exhaust all edge-cases of the program.

In this case, the use of AFL allows us to obtain thousands of “realistic” households in only a few hours of continuous testing on a fairly powerful machine. Another utility, afl-cmin then allows us to remove duplicates testing the same paths in the binary to arrive at a minimal test set that offers an optimal coverage of the starting program. This minimized corpus contains a few hundred test sets for the 2018 and 2019 versions of the income tax calculation.

Although these “realistic” test sets usually contain completely unrealistic income combinations for a tax household, they have the advantage of being diverse enough to handle all the different combinations of situations for the calculation of income tax, which would be difficult to achieve when writing the test sets by hand. Therefore, it might be preferable for lawyers who write the trial sets to use tax households found by fuzzing rather than inventing them, in order to have an optimal validation of the implementation of the income tax calculation.

Domain-specific languages for critical software

During this long journey under the hood of the engine that underlies the DGFiP’s income tax calculation, we encountered a whole zoo of exotic languages and techniques derived from formal methods. I would like to end this post by taking a step back and pointing out some fundamental reasons why dedicated languages and formal methods are a very powerful tool to ensure the optimal quality of critical software over the long term.

The difficulty of long-term code maintenance

No software, unlike diamonds, lasts forever. But some, because of the crucial objectives they accomplish, are intended to be used for an indefinite period of time. In the 1960s and 1970s, banking institutions around the world computerized their transaction management systems using the COBOL programming language. Sixty years later, COBOL is no longer taught at universities and is widely considered obsolete, but banks still use it to run the global economy The choice of a programming language is necessary to start a project. But even when choosing a language that is popular today, one is not immune to the computer zeitgeist that has made many languages, frameworks and technologies obsolete.

Considered on time scales of the duration of several careers, it is unlikely that a technology of today will still be taught at university in 70 or 80 years. And as the original programmers retire, it becomes impossible to rely on the labour market to provide a skilled, job-ready workforce.

What strategies should be adopted to guard against obsolescence in such long-term projects? A first solution is available to very large organizations: the creation of a generalist in-house language. This is the case of the Ada language, created in the 1980s by the US Department of Defense (DoD). By imposing the use of this language in all its projects, the DoD was able to create, from scratch, a demand for Ada programmers sufficient for the Ada community to reach critical mass allowing it to survive in the long term. With enough users and long term funding, Ada has been able to receive many updates and its tooling continues to adapt to modern trends in programming languages.

Agility by using dedicated languages

However, not all organizations have the size, the level of planning and funding that the U.S. Department of Defense commands. Therefore, a second strategy might be relevant for smaller projects that also have constraint of long-term code maintenance.

What the DGFiP example teaches us is that, thanks to the use of a dedicated language, only two part-time PhD students are needed to modernize a compiler; compare this with the work required to port a code base. Of course, it is always easier for an IT project manager to recruit a mass of low-skilled developers than to find and retain profiles with specific skills such as those possessed by Raphaël and me (namely a Masters in Computer Science with a Compilation and/or Theory major).

Nonetheless, a dedicated language with a compiler well mastered by specialists trained in formal methods is a formidable assurance of the project’s future and interoperability. Basically, an agile dedicated language that adapts to functional requirements and the passage of time multiplies the expressiveness of the code base. In reality, code and language form a coherent whole: only the execution of the code according to the semantics of the language matters.

With an established general-purpose language such as C or Java, you only have the power to change the code to adapt and modify your software. With a dedicated language and a well-tested compiler, the language itself becomes a tool at the service of the software’s evolution, and no longer a necessary evil to choose at the beginning which would inevitably turn into insurmountable levels of technical debt anyway.

What about M: this dedicated language is now 30 years old. Does our modernization proposal have the potential to last that long? It’s impossible to know in advance, but what we can say is that the foundations on which M and M++ are built are far stronger than those on which M had been written in 1990. With clear semantics, a compiler written in a functional language and structured according to a clear and extensible architecture, the language benefits from the evolution of 30 years of good practices in compiler theory and formal methods.

Beware, a dedicated language can become a double-edged sword without the right skillset! You shouldn’t be changing the semantics of a language on the spur of the moment, because a tiny change can break the entire code base. For this reason, compiler engineers and formal methods specialists, far from being rendered obsolete by statistical learning methods, remain and will remain for a very long time absolutely crucial. The study of programming languages, compiler theory and formal methods provide a real specific skill that is extremely useful for many critical computing projects.

Conclusion: have confidence in language artisans

In a more figurative sense, the choice of the dedicated language and its associated competence in formal methods can be compared to the choice of craftsmanship in relation to an industrial process of porting code from one language to another. Craftsmanship has a long tradition of transmitting knowledge over the long term, based on a small number of independent practitioners trained in high-level skills with relative versatility. In contrast, the industry aims to transform the production process into a fairly rigid chain of standardized tasks performed by low-skilled workers. Like other production sectors, information technology tends to follow this process of industrialization over the course of the time.

But industrialization requires critical mass and often the search for infinite growth. This analogy also applies to the programming languages. So before reluctantly choosing an established language for your long term IT project, ask yourself if you really want to be part of an industrial logic of infinite growth, or if it is not more opportune to entrust its realization to language craftsmen, who will be able to produce and maintain beautiful software from the terroir!